幻方算法（Magic Square）

winston

一、幻方按照阶数可分成了三类，即奇数阶幻方、双偶阶幻方、单偶阶幻方。
二、奇数阶幻方（劳伯法）
奇数阶幻方最经典的填法是罗伯法。填写的方法是：
把1（或最小的数）放在第一行正中；按以下规律排列剩下的(n×n－1)个数：

（1）每一个数放在前一个数的右上一格；

（2）如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；



（3）如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；

（4）如果这个数所要放的格已经超出了顶行且超出了最右列，那么就把它放在底行且最左列；


（5）如果这个数所要放的格已经有数填入，那么就把它放在前一个数的下一行同一列的格内。
例，用该填法获得的5阶幻方：

17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

二、双偶数阶幻方（海尔法）
所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方，即4K阶幻方。在说解法之前我们先说明一个“互补数”定义：就是在n阶幻方中，如果两个数的和等于幻方中最大的数与1的和（即n×n＋1），我们称它们为一对互补数。如在三阶幻方中，每一对和为10的数，是一对互补数 ；在四阶幻方中，每一对和为17的数，是一对互补数。
双偶数阶幻方最经典的填法是海尔法。填写的方法是：
以8阶幻方为例：
（1）先把数字按顺序填。然后，按4×4把它分割成4块（如图）

1	2	3	4	5	6	7	8
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
25	26	27	28	29	30	31	32
33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
57	58	59	60	61	62	63	64

（2）每个小方阵对角线上的数字（如左上角小方阵部分），换成和它互补的数。

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

三、单偶数阶幻方（斯特拉兹法）
所谓单偶阶幻方就是当n不可以被4整除时的偶阶幻方，即4K+2阶幻方。如(n=6，10，14……)的幻方。


单偶数阶幻方最经典的填法是斯特拉兹法。填写的方法是：
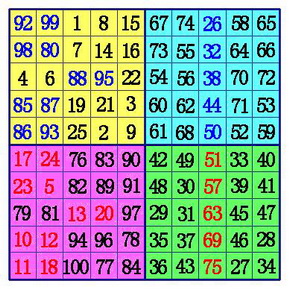
以10阶幻方为例。这时，k=2。
（1）把魔方阵分为A，B，C，D四个象限，这样每一个象限肯定是奇数阶。用罗伯法，依次在A象限，D象限，B象限，C象限按奇数阶幻方的填法填数。


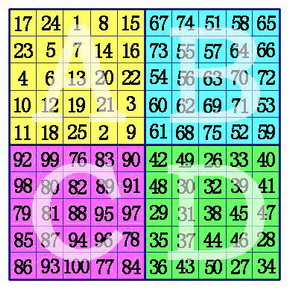
（2）在A象限的中间行、中间格开始，按自左向右的方向，标出k格。A象限的其它行则标出最左边的k格。将这些格，和C象限相对位置上的数互换位置。


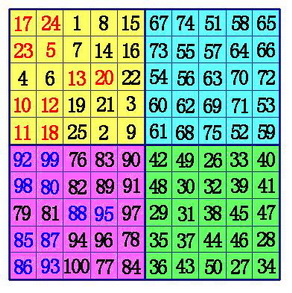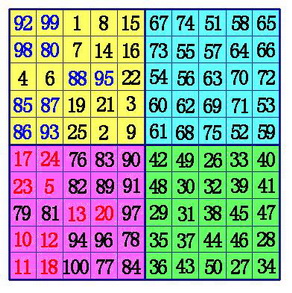
（3）在B象限所有行的中间格，自右向左，标出k－1格。(注：6阶幻方由于k－1=0，所以不用再作B、D象限的数据交换)，将这些格，和D象限相对位置上的数互换位置。

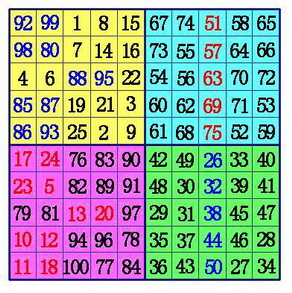
四、源代码如下，已加详细注释

1. #include<stdio.h>
2. #include<stdlib.h>
4. int array[15][15];
6. int init(int degree)                                  //初始化
7. {
8.         int i;
9.         int j;
10.        
11.         for(i=0; i<=degree+1; i++)
12.         for(j=0; j<=degree+1; j++)
13.                 array[i][j] = 0;
14.         return 0;
15. }
17. int test_print(int x, int y, int w, int h)            //测试用的，输出以（x，y）为原点，宽为w，高为h，这个区域的数值
18. {
19.         int i;
20.         int j;
21.         for(i=y; i<=y+h-1; i++){
22.                 for(j=x; j<=x+w-1; j++){
23.                         printf("%2d ",array[i][j]);
24.                 }
25.                 printf("\n");
26.         }
27.         return 0;
28. }
30. int lao_bo_er(int degree, int x, int y, int num)      //劳伯法
31. {
32.         int i;
33.         int j;
34.         int k;
35.        
36.         i = y;
37.         j = degree/2 + x;
38.         for(k=num; k<=num+degree*degree-1; k++){
39.                 array[i][j] = k;
40.                 if((k-num+1)%degree == 0){            //如果这个数所要放的格已经有数填入
41.                         i = (i-y+1)%degree+y;
42.                 }
43.                 else{                                 //每一个数放在前一个数的右上一格
44.                         i = (i-y-1+degree)%degree+y;
45.                         j = (j-x+1)%degree+x;
46.                 }
47.         }
48.         return 0;
49. }
51. int seq_range(int degree)                             //把数字按顺序填
52. {
53.         int i;
54.         int j;
55.         int num;
56.        
57.         num = 1;
58.         for(i=1; i<=degree; i++){
59.                 for(j=1; j<=degree; j++){
60.                         array[i][j] = num++;
61.                 }
62.         }
63.         return 0;
64. }
66. int si_te_la_zi(int degree, int x, int y, int num)    //斯特拉兹法
67. {
68.         int deg;
69.         int k;
70.         int temp;
71.         int i;
72.         int j;
73.        
74.         deg = degree/2;
75.         lao_bo_er(deg, x, y, num);                    //用罗伯法，依次在A象限，D象限，B象限，C象限按奇数阶幻方的填法填数
76.         lao_bo_er(deg, x+deg, y, num+2*deg*deg);
77.         lao_bo_er(deg, x, y+deg, num+3*deg*deg);
78.         lao_bo_er(deg, x+deg, y+deg, num+deg*deg);
80.         k = (degree-2)/4;
81.         for(i=1; i<=deg; i++){                        //A象限和C象限对换数据
82.                 for(j=1; j<=k; j++){
83.                         temp = array[i][j];
84.                         array[i][j] = array[i+deg][j];
85.                         array[i+deg][j]=temp;
86.                 }
87.                 for(j=deg+deg/2+1; j>=deg+deg/2-k+3; j--){
88.                         temp = array[i][j];
89.                         array[i][j] = array[i+deg][j];
90.                         array[i+deg][j]=temp;
91.                 }
92.         }
93.        
94.         for(i=j=1; j<=deg/2+k; j++){                  //B象限和D象限对换数据
95.                 temp = array[i+deg/2][j];
96.                 array[i+deg/2][j] = array[i+deg+deg/2][j];
97.                 array[i+deg+deg/2][j]=temp;
98.         }
99.        
100.         return 0;
101. }
103. int hai_er_fa(int degree)                             //海尔法
104. {
105.         int i;
106.         int j;
107.         int complement;
108.         int deg;
109.        
110.         seq_range(degree);
111.        
112.         complement = degree*degree+1;
113.         deg = degree/4;
114.         for(i=0; i<deg; i++){
115.                 for(j=0; j<deg; j++){                 //对角线上的数字换成和它互补的数
116.                         array[i*4+1][j*4+1] = complement - array[i*4+1][j*4+1];
117.                         array[i*4+1][j*4+4] = complement - array[i*4+1][j*4+4];
118.                         array[i*4+4][j*4+1] = complement - array[i*4+4][j*4+1];
119.                         array[i*4+4][j*4+4] = complement - array[i*4+4][j*4+4];
120.                        
121.                         array[i*4+2][j*4+2] = complement - array[i*4+2][j*4+2];
122.                         array[i*4+2][j*4+3] = complement - array[i*4+2][j*4+3];
123.                         array[i*4+3][j*4+2] = complement - array[i*4+3][j*4+2];
124.                         array[i*4+3][j*4+3] = complement - array[i*4+3][j*4+3];
125.                 }
126.         }
127.         return 0;
128. }
130. int main()
131. {
132.         int degree;
133.         printf("please input the degree\n");
134.         scanf("%d",°ree);
135.         init(degree);
136.         if(degree%2 == 1){                            //奇数阶幻方
137.                 lao_bo_er(degree,1,1,1);
138.                 test_print(1,1,degree,degree);
139.         }
140.         else if(degree%4 == 2){                       //双偶阶幻方
141.                 si_te_la_zi(degree, 1, 1, 1);
142.                 test_print(1,1,degree,degree);
143.         }
144.         else{                                         //单偶阶幻方
145.                 hai_er_fa(degree);
146.                 test_print(1,1,degree,degree);
147.         }
148.        
149.         return 0;
150. }

复制代码

作者：xuyuanfan77 发表于2011-12-27 1:06:42 原文链接